ARITHMATIC FOR COMPUTERS

1.NUMBER SYSTEMS

Binary Digits

A Binary Digit can only be 0 or 1

Binary Number

A Binary Number is made up Binary Digits.

More Than One Digit

So, there are only two ways you can have a binary digit ("0" and "1", or "On" and "Off") ... but what about 2 or more binary digits?

Let's write them all down, starting with 1 digit (you can test it yourself using the switches):

2 ways to have one digit ...

... 4 ways to have two digits ...

0	0	→	00
0	1	→	01
1	0	→	10
1	1	→	11

... 8 ways to have three digits ...

0	0	0	→	000
	0	1	→	001
	1	0	→	010
	1	1	→	011
1	0	0	→	100
	0	1	→	101
	1	0	→	110
	1	1	→	111

... and 16 ways to have four digits.

0	0	0	0	→	0000
		0	1	→	0001
		1	0	→	0010
		1	1	→	0011
	1	0	0	→	0100
		0	1	→	0101
		1	0	→	0110
		1	1	→	0111
1	0	0	0	→	1000
		0	1	→	1001
		1	0	→	1010
		1	1	→	1011
	1	0	0	→	1100
		0	1	→	1101
		1	0	→	1110
		1	1	→	1111

And, in fact, we have created the first 16 binary numbers:

Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Binary:	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111

Decimals

A Decimal Number (based on the number 10) contains a Decimal Point.

The value of the assigned weight is composed by 10 digits starting from 0 till 9

Decimal number is a base of 10.

First, let's have an example:

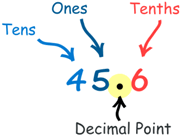
Here is the number "forty-five and six-tenths" written as a decimal number:

The decimal point goes between units and tenths.

45.6 has 4 tens, 5 units and 6 tenths, like this:

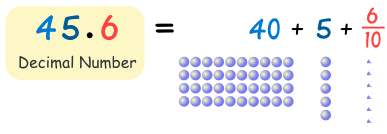
Now, let's discover how it all works ...

Place Value

It is all about Place Value !

When we write numbers, the position (or "place") of each digit is important.

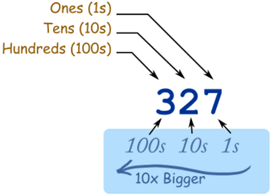
In the number 327:

the "7" is in the Units position, meaning just 7 (or 7 "1"s),
the "2" is in the Tens position meaning 2 tens (or twenty),
and the "3" is in the Hundreds position, meaning 3 hundreds.

"Three Hundred Twenty Seven"

	As we move left, each position is 10 times bigger!
	Example: Hundreds are 10 times bigger than Tens

... and ...

As we move right, each position is 10 times smaller.
From Hundreds, to Tens, to Units

But what if we continue past Units?

What is 10 times smaller than Units?

1/10 ths (Tenths) are!

But we must first write a decimal point, so we know exactly where the Units position is: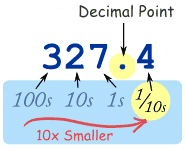
"three hundred twenty seven and four tenths" but we usually just say "three hundred twenty seven point four"

And that is a Decimal Number!

Hexadecimals

A Hexadecimal Number is based on the number 16

16 Different Values

There are 16 Hexadecimal digits. They are the same as the decimal digits up to 9, but then there are the letters A, B, C, D, E and F in place of the decimal numbers 10 to 15:

Hexadecimal:	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

So a single Hexadecimal digit can show 16 different values instead of the normal 10.

As we move left, every number place is 16 times bigger.

Example: What is the decimal value of the hexadecimal number "D1CE"

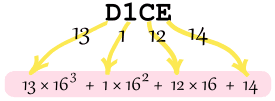
= 53,248 + 256 + 192 + 14
= 53,710

The Point !

Example: 2E6.A3

This is 2×16×16 + 14×16 + 6 + 10/16 + 3/(16×16)
Read below to find out why

Numbers can be placed to the left or right of the point, to indicate values greater than one or less than one:

	The number just to the left of the point is a whole number, we call this place units. As we move left, every number place its 16 times bigger.

	The first digit on the right of the point means sixteenths (1/16). As we move further right, every number place its 16 times smaller (one sixteenth as big). NUMBER SYSTEM CONVERSION CONVERT A BINARY,OCTAL OR HEXADECIMAL NUMBER TO DECIMAL

CONVERT A DECIMAL NUMBER TO BINARY, OCTAL AND HEXADECIMAL

2.NUMBER OPERATION

BASIC BINARY OPERATION

BASIC BINARY NUMBER OPERATION

binary number operation is a bit different from what we do in normal mathematic operation. Binary number system only contain TWO numbers which are 1 and 2.

++++++ADDITION ++++++++

There are four simply rule that we must follow......

RULES

0+0=0

0+1=1

1+0=1

1+1=10

1+1+1=11

THE RULES OF ADDITION

Let we have some example to make it clear..

1 <------------- This is call carried bit

11 (like normal addition, the second digit will stay,other will be carried forward)

+ 1 COLUMN 1: use 1+1=10... WRITE 0..... 1 carry forward..

100 COLUMN 2: use 1+1=10......WRITE 10...

--------------SUBTRACTION----------

For subtraction,there are also some simply rules to follow....

RULES

0-0=0

0-1=1

( borrow from the next binary number)

1-0=1

1-1=0

THE RULE FOR SUBTRACTION

02 <------if cant minus 0 with 1, borrow from left side number)

101 COLUMN 1 : use 1-0=1...... WRITE 1...

‾ 10 COLUMN 2: cannot minus 1 with 0.... borrow 2 from left side number 1.. the

11 1 become 0... 2 minus 1.. WRITE 1..

COLUMN 3: after borrow by 0.... left only zero... so no need write.

* * * * MULTIPLICATION * * * *

For binary multiplication we only need to follow few rules below ...

Rules of Multiplication

0 x 0 = 0

0 x 1 = 0

1 x 0 = 0

1 x 1 = 1

example of binary multiplication :

  101
  x11
   101 < firstly, we multiply 101 to 1

1010 < Then we put a 0 as a placeholder as we would in decimal multiplication, and multiply 101 by 1

1111 < at the end, we add 101 to 1010 then we can get the answer

÷ ÷ ÷ ÷ ÷ ÷ DIVISION ÷ ÷ ÷ ÷ ÷ ÷

Division is easy and involves our knowledge of binary multiplication.
example of binary division of 1011 into 11

                 11   R=10
        11 )1011
              -11
               101
                -11
                  10  <-- remainder, R

      To check our answer, we can multiply our divisor 11 by our quotient 11. Then we add its' product to the remainder 10, and compare it to our dividend of 1011.

          11
      x 11
       11
       11
     1001  < product of 11 and 11

   1001
+ 10  < remainder 10
    1011  < sum of product and remainder

The sum is equal to our initial dividend, therefore our solution is correct.

here are some link that can refer...
http://www.ustudy.in/node/7598
http://www.exploringbinary.com/binary-multiplication/

HOW TO MULTIPLY BINARY NUMBERS

HEXADECIMAL NUMBER OPERATION

++++HEXADECIMAL ADDITION++++

Unlike decimal system (base 10) with 10 digits and also binary system (base 2) with two digits, hexadecimal system (base 16) has 16 digits for its operation.

DECIMAL	4-BIT BINARY	HEXADECIMAL
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

Comparison between decimal, binary, and hexadecimal system…

Note: for hexadecimal system, from number 10 start we represent with alphabet A until number 16 and alphabet F. Let do some exercise !!

5 8₁₆

+2 2₁₆

7 10_{16 <---- Final answer will write 7A base 16.}

Column 1 : Like decimal system, 8+2=10..... BUT the 1 will not carry out.. It will stay...
Column 2 : Do 5+2=7.....
Column 3: Final step.... convert the number 10 into hexadecimal format... which is A.... DONE !!!

::::::::::Another example which are more complicated:::::

	D	F₁₆
+	A	C₁₆

	13₁₀+10₁₀+1₁₀=24₁₀	15₁₀+12₁₀=27₁₀
	24_10-16₁₀=8₁₀	27₁₀-16₁₀=11₁₀
	=8₁₆
	1 will carry	1 will carry

Column 1: F+C=15+12=27.... But remember in hexadecimal system, only have 16 digits.. So we need use 27-16=11. The number 11 in hexadecimal system,so no need subtract again. Once we subtract one time, we need carry 1.
Column 2: We solve D+A+1 = 13+10+1 = 24. Once again 24 exceed 16 digits in hexadecimal system... So we use same method in column 1, and we will get 8 and 1 will be carry.
Final step, we write the answer as 18B_16...

----------HEXADECIMAL SUBTRACTION--------

For subraction, we need do more conversion in order to solve the question. We need to convert hexadecimal number into binary number, then we need find 2's complement. Convert back into hexadecimal number then number then add two number. NOT UNDERSTAND ????!!! Come we do an example together.....

EX.......

84₁₆-2A₁₆

_{....1's compliment of}2A_{16 = 0101010}

_{..... 2's compliment of}2A_{16 = 0101010+1---->11010110}

_{......convert back into hexadecimal number ------> +}D6₁₆

_{........Then add two number together, FOLLOW WHAT WE HAD DONE ABOVE, which we will get}15A_{16.... BUT we will drop the 1, cause the 1 represent negative in 2's compliment .}

_{....... So final answer is}5A_16.

_{Finally we have some links and video that maybe helpful to you all to understand more.}

_{http://www.mathsisfun.com/hexadecimals.html.........}

_{http://www.exploringbinary.com/binary-multiplication/.............}

_{http://www.sqa.org.uk/e-learning/CompArch01CD/page_21.htm..........}

http://www.ustudy.in/node/7598

_{We also include some youtube video ..}

_{ADDING AND SUBTRACTING IN HEXADECIMAL}

-megat ahmad mustaqim-

B031310390

COMPUTER ORGANIZATION AND ARCHITECTURE

Pages

Thursday 12 December 2013

ARITHMATIC FOR COMPUTERS

Binary Digits

Binary Number

More Than One Digit