Memory Organization : Cache Memory

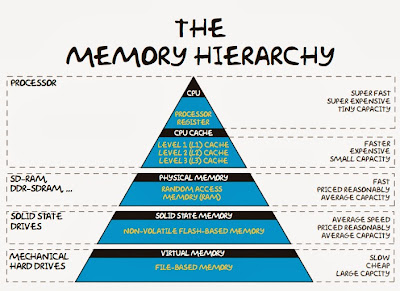
What do we want in a memory ?

We’d like to have a memory system that performs like 2-10 GB of fast SRAM typical SRAM sizes are in MB, not GB .
Costs like 1-4 GB of DRAM (slower) typical DRAMs are order of magnitude slower than SRAM

Hint : Use a hierarchy of memory technologies

Cache Analogy :)

Consider the following analogy of caching. You are planning to write a very long paper on the history of mythology of many different cultures. You start with ancient Babylonian myths, and work your way to Greek, Roman, Norse, Native American, Asian, etc. myths. You've divided your paper so that each chapter covers one culture's mythology. Thus, at any one time, you are studying one mythology.

You have a computer on your desk, and get your books online. You can download only so many books because your computer is limited in memory. The advantage of downloading the books onto your own computer is so that you can access the material quickly. Downloading the books is quite slow, so you hope not to do it very often.

If it weren't for the fact that you collect related books and write on those books for each chapter (say, 10 books on Greek mythology, then 10 books on Norse mythology), you might be forever downloading books. Even though the majority of books remain at the central library site, the books you need are on your computer, which is quick to access.

What happens if you have already downloaded 10 books (assuming they all take the same amount of space), and you want an 11th book? You will need to delete one of your books off your computer, to make room for the next book.

Which one should you pick? You could pick the one that you haven't read in the longest time. That policy is called "least recently used". Or you could see which book you've had on your computer the longest time. That policy is called "first in first out". Or perhaps the one you've looked at least. That's called "least frequently used".

In any case, you use some policy to decide which book to get rid of to make space for the new books.

"source http://www.cs.umd.edu/class/sum2003/cmsc311/Notes/Memory/introCache.html"

Directed Mapped Cache :)

Location determined by address . Direct mapped is only one choice.

1. How do we know which particular block is stored in a cache location?

Store block address as well as the data
Actually, only need the high-order bits ◦ Called the tag

2. What if there is no data in a location?

Valid bit: 1 = present, 0 = not present . Initially 0

Example of Cache :)

8-blocks, 1 word/block, direct mapped
(Initial state)

Measuring Cache Performance :)

-Emran Bin Rahmad-

B031310405

ARITHMATIC FOR COMPUTERS

1.NUMBER SYSTEMS

Binary Digits

A Binary Digit can only be 0 or 1

Binary Number

A Binary Number is made up Binary Digits.

More Than One Digit

So, there are only two ways you can have a binary digit ("0" and "1", or "On" and "Off") ... but what about 2 or more binary digits?

Let's write them all down, starting with 1 digit (you can test it yourself using the switches):

2 ways to have one digit ...

... 4 ways to have two digits ...

0	0	→	00
0	1	→	01
1	0	→	10
1	1	→	11

... 8 ways to have three digits ...

0	0	0	→	000
	0	1	→	001
	1	0	→	010
	1	1	→	011
1	0	0	→	100
	0	1	→	101
	1	0	→	110
	1	1	→	111

... and 16 ways to have four digits.

0	0	0	0	→	0000
		0	1	→	0001
		1	0	→	0010
		1	1	→	0011
	1	0	0	→	0100
		0	1	→	0101
		1	0	→	0110
		1	1	→	0111
1	0	0	0	→	1000
		0	1	→	1001
		1	0	→	1010
		1	1	→	1011
	1	0	0	→	1100
		0	1	→	1101
		1	0	→	1110
		1	1	→	1111

And, in fact, we have created the first 16 binary numbers:

Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Binary:	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111

Decimals

A Decimal Number (based on the number 10) contains a Decimal Point.

The value of the assigned weight is composed by 10 digits starting from 0 till 9

Decimal number is a base of 10.

First, let's have an example:

Here is the number "forty-five and six-tenths" written as a decimal number:

The decimal point goes between units and tenths.

45.6 has 4 tens, 5 units and 6 tenths, like this:

Now, let's discover how it all works ...

Place Value

It is all about Place Value !

When we write numbers, the position (or "place") of each digit is important.

In the number 327:

the "7" is in the Units position, meaning just 7 (or 7 "1"s),
the "2" is in the Tens position meaning 2 tens (or twenty),
and the "3" is in the Hundreds position, meaning 3 hundreds.

"Three Hundred Twenty Seven"

	As we move left, each position is 10 times bigger!
	Example: Hundreds are 10 times bigger than Tens

... and ...

As we move right, each position is 10 times smaller.
From Hundreds, to Tens, to Units

But what if we continue past Units?

What is 10 times smaller than Units?

1/10 ths (Tenths) are!

But we must first write a decimal point, so we know exactly where the Units position is:
"three hundred twenty seven and four tenths" but we usually just say "three hundred twenty seven point four"

And that is a Decimal Number!

Hexadecimals

A Hexadecimal Number is based on the number 16

16 Different Values

There are 16 Hexadecimal digits. They are the same as the decimal digits up to 9, but then there are the letters A, B, C, D, E and F in place of the decimal numbers 10 to 15:

Hexadecimal:	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

So a single Hexadecimal digit can show 16 different values instead of the normal 10.

As we move left, every number place is 16 times bigger.

Example: What is the decimal value of the hexadecimal number "D1CE"

= 53,248 + 256 + 192 + 14
= 53,710

The Point !

Example: 2E6.A3

This is 2×16×16 + 14×16 + 6 + 10/16 + 3/(16×16)
Read below to find out why

Numbers can be placed to the left or right of the point, to indicate values greater than one or less than one:

	The number just to the left of the point is a whole number, we call this place units. As we move left, every number place its 16 times bigger.

	The first digit on the right of the point means sixteenths (1/16). As we move further right, every number place its 16 times smaller (one sixteenth as big). NUMBER SYSTEM CONVERSION CONVERT A BINARY,OCTAL OR HEXADECIMAL NUMBER TO DECIMAL

CONVERT A DECIMAL NUMBER TO BINARY, OCTAL AND HEXADECIMAL

2.NUMBER OPERATION

BASIC BINARY OPERATION

BASIC BINARY NUMBER OPERATION

binary number operation is a bit different from what we do in normal mathematic operation. Binary number system only contain TWO numbers which are 1 and 2.

++++++ADDITION ++++++++

There are four simply rule that we must follow......

RULES

0+0=0

0+1=1

1+0=1

1+1=10

1+1+1=11

THE RULES OF ADDITION

Let we have some example to make it clear..

1 <------------- This is call carried bit

11 (like normal addition, the second digit will stay,other will be carried forward)

+ 1 COLUMN 1: use 1+1=10... WRITE 0..... 1 carry forward..

100 COLUMN 2: use 1+1=10......WRITE 10...

--------------SUBTRACTION----------

For subtraction,there are also some simply rules to follow....

RULES

0-0=0

0-1=1

( borrow from the next binary number)

1-0=1

1-1=0

THE RULE FOR SUBTRACTION

02 <------if cant minus 0 with 1, borrow from left side number)

101 COLUMN 1 : use 1-0=1...... WRITE 1...

‾ 10 COLUMN 2: cannot minus 1 with 0.... borrow 2 from left side number 1.. the

11 1 become 0... 2 minus 1.. WRITE 1..

COLUMN 3: after borrow by 0.... left only zero... so no need write.

* * * * MULTIPLICATION * * * *

For binary multiplication we only need to follow few rules below ...

Rules of Multiplication

0 x 0 = 0

0 x 1 = 0

1 x 0 = 0

1 x 1 = 1

example of binary multiplication :

  101
  x11
   101 < firstly, we multiply 101 to 1

1010 < Then we put a 0 as a placeholder as we would in decimal multiplication, and multiply 101 by 1

1111 < at the end, we add 101 to 1010 then we can get the answer

÷ ÷ ÷ ÷ ÷ ÷ DIVISION ÷ ÷ ÷ ÷ ÷ ÷

Division is easy and involves our knowledge of binary multiplication.
example of binary division of 1011 into 11

                 11   R=10
        11 )1011
              -11
               101
                -11
                  10  <-- remainder, R

      To check our answer, we can multiply our divisor 11 by our quotient 11. Then we add its' product to the remainder 10, and compare it to our dividend of 1011.

          11
      x 11
       11
       11
     1001  < product of 11 and 11

   1001
+ 10  < remainder 10
    1011  < sum of product and remainder

The sum is equal to our initial dividend, therefore our solution is correct.

here are some link that can refer...
http://www.ustudy.in/node/7598
http://www.exploringbinary.com/binary-multiplication/